Tying knots with reflecting lightrays
These knots seem to be called billiard knots in the literature. They coincide with Lissajous knots as shown by Jones and Przytycki in "Lissajous knots and billiard knots", Banach center Publications 42, 145-163 (1998). Lissajous knots are knots admitting a parametrization of the form $(\cos(n_x t + d_x), \cos(n_y t + d_y), \cos(n_z t + d_z))$. There are strong constraints on such knots (see the wikipedia), and for example no torus knot can be Lissajous.
This started as a comment, but outgrew the space.
Edit1, 3(a) vs Edit2, (3) on their face sound like different questions to me: (forevery knot is there a polyhedron), vs. (is there a polyhedron such that forevery knot) for which the knot is a billiard trajectory.
From a solution to Edit1, 3(a), you can get a convex set that works as in Edit2,3, but I don't see why a polyhedron would be implied. If 3(a) is true, then take a countable sequence of polyhedra together with billiard trajectories that cover all possible knot types. Take a sequence of points on $\mathbb {RP}^2$ with disjoint neighborhoods of radius $\epsilon_i$. Now compress the $i$th polyhedron by an affine map until the points of contact with the knot are nearly on a pair of parallel planes with tangent planes nearly parallel to that plane, and graft this in to $S^2$ near the pair of antipodal points representing the $i$th point chosen in $\mathbb{RP}^2$.
There is an implication that forevery knot there is a convex set ... implies forevey knot there is a polyhedron ... . A convex set that works for a knot, or finite collection of knots, can be modified to a polyhedron: just use the tangent planes at the points of contact to delineate a polyhedron.
My guess is that: 3(a) is true. I'm imagining taking a picture of a knot as a plait, and then constructing a convex tube just for it, where the knot mostly bounces up and down toward you and away from you, but bends and crosses where necessary. If I get a concrete construction, I'll fill in specifics --- currently it's just an idea. I would also guess that no single polyhedron will work for all knots. It's an interesting challenge to try to describe special properties of knots associated with a specific polyhedron.
Added: Plan for realizing all knots with one polyhedron
On further reflection (ha ha), my guess is that we can construct a single polyhedron that will realize all possible knot types. I will sketch the plan --- others are welcome to join in to either fill it in, or refute it.
Update: See Joseph O'Rourke's answer for pictures.
To start, think of a planar polygon that is a slightly modified square. In a square, there are trajectories that bounce back and forth nearly perpendicular to two parallel walls, gradually proceeding down the length. When they reach the end, they glance across a wall and start a journey back.
Now modify the square by beveling one corner at a 45 degree angle, so that when trajectories reach the cutout, they strike at an angle just less than 45 degrees from perpendicular, so they turn nearly 90 degrees and start in the nearly perpendicular direction, with a slight drift away from the nearby side. Trajectories bounce back and forth for a time between the two major directions, hitting the bevel every other turn, until they reach the end of the bevel, when they start a journey crisscorssing between the second pair of parallel sides.
Put another 45 degree bevel at the opposite corner, so now there are periodic trajectories with this qualitative description with arbitrarily many crossings between pairs of parallel sides.
I have a strong hunch that any knot type can be arranged in a form that has projection to one of these trajectories, just making use of the main weaving part for creating the knot type, but I haven't thought through the details. Let's suppose so, or at least suppose we have a knot that has a weaving style projection.
Now, make a cylinder with the hexagon as above as base, adding two new faces perpendicular to the faces of the cylinder. It is best to visualize it as a thin plate, although logically it is irrelevant how high it is. Trajectories in the cylinder map to trajectories in the hexagon. For each closed trajectory $\gamma$ in the hexagon and for each integer $N$, there is a circle's worth of trajectories in 3 dimensions that project to $\gamma$ and hit the floor and ceiling exactly $N$ times (at regular intervals). The extra circle parametrizes their phase.
Lemma : for any $\gamma$ and any specification of crossing information, there is a billiard trajectory that projects to $\gamma$ and has the given types of crossings.
I suspect this is probably reflexive knowledge to some group of mathematicians. It's saying that if you take a collection $H$ of numbers in the interval (the vertical heights), then look at their orbit under the semigroup $\{ N x + b\}$ generated by translations and multiplication by integers, then the ordering of Sawtooth(Nx + b)(H) can be anything. I think a stronger fact is true the images should be dense in the set of $|H|-tuples$ in the interval.
If this plan holds up, then every knot type can be realized in this 8-faced polyhedron.
This is my understanding of Bill Thurston's ingenious idea:
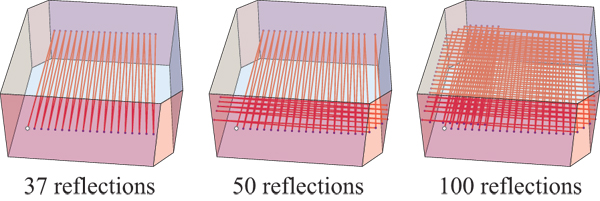
I selected the initial ray to drift upward slowly, and did not run the simulation so far as to reflect off the ceiling.
As per Bill's request, here is an overhead view of that rightmost image above, with rays colored
to more clearly distinguish the reflecting planes.
