Trigonometry Identity: Prove that $\sin(a-b)=\sin a \cos b - \cos a \sin b$
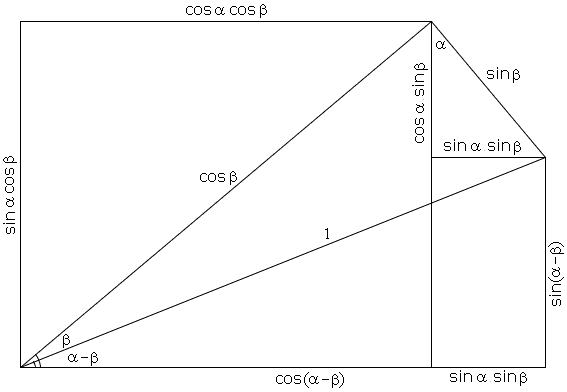
Something to help you visualize this geometrically.
The simplest way of deriving/proving this is through Euler's formula:
Take $e^{i(\theta+\alpha)}$ which, through basic exponent rules we know is equal to $e^{i\theta +i\alpha} = e^{i\theta}\cdot e^{i\alpha}\ .$ Now expanding this (using Euler's formula) we get: $$\begin{align} e^{i\theta}\cdot e^{i\alpha} &= (\cos(\theta)+i\sin(\theta))\cdot(\cos(\alpha)+i\sin(\alpha))\\ &= \cos(\theta)\cos(\alpha)-\sin(\theta)\sin(\alpha) + i(\cos(\theta)\sin(\alpha)+\sin(\theta)\cos(\alpha))\ \\ \end{align}$$ and $$\begin{align} e^{i(\theta + \alpha)} = \cos(\theta + \alpha) + i \sin(\theta + \alpha) \end{align}\ .$$ Remembering that $e^{i(\theta +\alpha)} = e^{i\theta}\cdot e^{i\alpha}\ $we can see that $$\cos(\theta)\cos(\alpha)-\sin(\theta)\sin(\alpha) + i(\cos(\theta)\sin(\alpha)+\sin(\theta)\cos(\alpha))\ = \cos(\theta + \alpha) + i \sin(\theta + \alpha)$$
and because we know that the real part has to equal the real part and the complex has to equal the complex we get two equations: $$\begin{align} \cos(\theta)\cos(\alpha)-\sin(\theta)\sin(\alpha) &= \cos(\theta + \alpha)\\ \cos(\theta)\sin(\alpha)+\sin(\theta)\cos(\alpha) &= \sin(\theta + \alpha)\ . \end{align} $$
Now we simply make $\alpha = -\phi$ and remember that $\sin(-\theta) = -\sin(\theta)$ and $\cos(-\theta) = \cos(\theta)$, to get our subtraction identities: $$\begin{align} \cos(\theta - \phi) &=\cos(\theta)\cos(-\phi)-\sin(\theta)\sin(-\phi) \\ &= \cos(\theta)\cos(\phi)+\sin(\theta)\sin(\phi)\\ \\ \sin(\theta -\phi ) &= \cos(\theta)\sin(-\phi)+\sin(\theta)\cos(-\phi) \\ &= -\cos(\theta)\sin(\phi)+\sin(\theta)\cos(\phi)\ \ \blacksquare \end{align} $$
Now I will provide my favorite proof of this identity, which i consider more intuitive than the one above.
First we construct three right triangles, with two of them placed so that the hypotenuse of the first one is congruent and adjacent to the base of the other, and the third is constructed from the top point of the second to the base of the first (perpendicular to it):

It is clear from this construction that we are looking for the $\sin(\beta + \delta)$, which is equal to $\frac{\overline{DE}}{\overline{DA}}$. We however want to put this into terms of our first two triangles, which we presumably know more about. Because the identity we are looking for is actually a circular identity, or rather is true for the unit circle, we will let $\overline{DA}$ be a radius of the unit circle (i.e with a measure of $1$). This further reduces $\frac{\overline{DE}}{\overline{DA}}$ to $\frac{\overline{DE}}{1}$, meaning $$\sin(\beta + \delta) = \overline{DE}\ .$$
We can now construct a line from point $C$ that is perpendicular to $\overline{DE}$, in order to divide up line $\overline{DE}$:

Now we can say that because $\overline{DE} = \overline{DF} + \overline{FE}$, and $\overline{FE} \cong \overline{CB}$ that $$\sin(\beta + \delta) = \overline{DE} = \overline{DF} + \overline{CB}\ \ .$$
Now we try to find $\overline{CB}$ in terms of triangles we know. Because we know that $\sin(\delta) = \frac{\overline{CB}}{\overline{CA}}$ we can say that $\overline{CB} =\sin(\delta)\cdot \overline{CA}$. Now we can try to find $\overline{CA}$; noticing that $\cos(\beta) = \frac{\overline{CA}}{DA} $, but because $\overline{DA} = 1$ we say $\cos(\beta) = \overline{CA}$, we can write $\overline{CB} =\sin(\delta)\cos(\beta)$. Finally substituting into our equation for $\sin(\delta + \beta)$ we get $$\sin(\delta + \beta) = \overline{DF} + \sin(\delta)\cos(\beta)\ .$$
Finally we must find $\overline{DF}$, which can be written in terms of the angle $\angle FDC$ as $\cos(\angle FDC) \cdot \overline{DC} = \overline{DF}$. We know that $\angle FDC = 90^{\bigcirc} - \angle DCF$, and we know that $\angle DCF = 90^{\bigcirc} - \angle FCA$, as well as that $ \angle FCA = 90^{\bigcirc} - \angle ACB$, and finally that $\angle ACB = 90^{\bigcirc} - \delta$. Now substituting appropriatly we get $$\angle FDC = \delta\ .$$ Which means that we can express $\cos(\angle FDC) \cdot \overline{DC} = \overline{DF}$ in terms of delta as follows $ \overline{DF} = \cos(\delta) \cdot \overline{DC}\ $ Because we know that $\overline{DC} = \sin(\beta)$ we can say $$\overline{DF} = \cos(\delta) \cdot \sin(\beta)\ .$$
Substituting into our $\sin(\delta + \beta)$ equation we get $$\sin(\delta + \beta) = \cos(\delta)\sin(\beta)+ \sin(\delta)\cos(\beta)\ .$$
Now we do as we did in our last proof and let $\beta = - \phi$ to get $$\begin{align} \sin(\delta -\phi ) &= \cos(\delta)\sin(-\phi)+\sin(\delta)\cos(-\phi) \\ &= -\cos(\delta)\sin(\phi)+\sin(\delta)\cos(\phi)\ \ \blacksquare \end{align} $$
EDIT: I just noticed you do not want arguments that use $\sin(\theta + \alpha)$, therefore I am going to make the first argument without $\sin(\theta + \alpha)$.
Take $e^{i(\theta-\alpha)}$ which, through basic exponent rules we know is equal to $e^{i\theta - i\alpha} = e^{i\theta}\cdot e^{-i\alpha}\ .$ Now expanding this (using Euler's formula) we get: $$\begin{align} e^{i\theta}\cdot e^{-i\alpha} &= (\cos(\theta)+i\sin(\theta))\cdot(\cos(-\alpha)+i\sin(-\alpha))\\ &= \cos(\theta)\cos(-\alpha)-\sin(\theta)\sin(-\alpha) + i(\cos(\theta)\sin(-\alpha)+\sin(\theta)\cos(-\alpha))\ \\ \end{align}$$ and $$\begin{align} e^{i(\theta - \alpha)} = \cos(\theta - \alpha) + i \sin(\theta - \alpha) \end{align}\ .$$ Remembering that $e^{i(\theta - \alpha)} = e^{i\theta}\cdot e^{-i\alpha}\ $we can see that $$\cos(\theta)\cos(-\alpha)-\sin(\theta)\sin(-\alpha) + i(\cos(\theta)\sin(-\alpha)+\sin(\theta)\cos(-\alpha))\ = \cos(\theta - \alpha) + i \sin(\theta - \alpha)$$
and because we know that the real part has to equal the real part and the complex has to equal the complex we get two equations, which simplify using $\sin(-\theta) = -\sin(\theta)$ and $\cos(-\theta) = \cos(\theta)$ : $$\begin{align} \cos(\theta)\cos(-\alpha)-\sin(\theta)\sin(-\alpha) &= \cos(\theta + \alpha) &\\ \cos(\theta)\cos(\alpha)+\sin(\theta)\sin(\alpha)&= &\\ \\ \cos(\theta)\sin(-\alpha)+\sin(\theta)\cos(-\alpha) &= \sin(\theta + \alpha) &\\ -\cos(\theta)\sin(\alpha)+\sin(\theta)\cos(\alpha) &=\ &\blacksquare \end{align} $$
Well, if you buy or have access to (through previous learning) $e^{i\theta} = \cos \theta + i \sin \theta$, then setting $\theta = a - b$ one has
$e^{i(a - b)} = \cos(a - b) + i\sin(a - b). \tag{1}$
But also,
$e^{i(a - b)} = e^{ia}e^{-ib} = (\cos a + i \sin a)(\cos b - i\sin b). \tag{2}$
The imaginary part of the product on the right of (20) is $\sin a \cos b - \cos a \sin b$; the imaginary part of $e^{(a - b)}$ is $\sin (a - b)$. Bringing these imaginary parts together (that is, equating them) yields
$\sin(a - b) = \sin a \cos b - \cos a \sin b. \tag{3}$
as was to be shown. QED.
Hope this helps. Cheerio,
and as always,
Fiat Lux!!!