The converse of Newton's shell theorem
Converse shell theorem for an exterior point mass:
Assume that the force ${\bf F}_{12}$ between two point masses $m_1$ and $m_2$ is collinear with the difference in positions ${\bf r}_{12}:={\bf r}_1-{\bf r}_2$, is central, and the magnitude $$|{\bf F}_{12}|=m_1m_2 f(|{\bf r}_{12}|)\tag{*}$$ is proportional to both the two point masses. We call the function $f(|{\bf r}_{12}|)$ the specific force.
Assume furthermore that the magnitude of the total force between an extended spherically symmetric mass $M$ and an exterior point mass $m$ is of the same form $$|{\bf F}|=mM f(r),\tag{**}$$ where $r\equiv |{\bf r}|$ is the distance between $m$ and the center of $M$.
Then the specific force $f$ is a linear combination of
a linear/Hooke force,
an inverse square/Newtonian gravity force.
Sketched proof: Let us use the same notation as the Wikipedia page. We consider the outside of a thin shell, i.e. $r\geq R$.
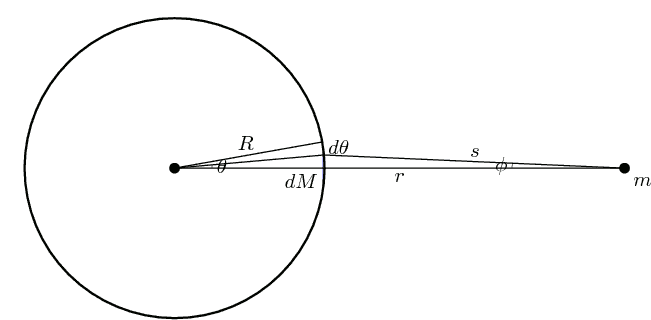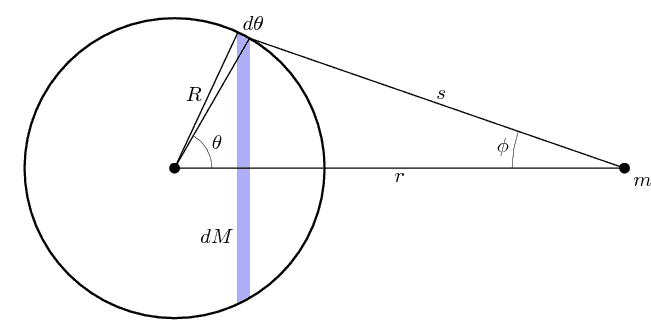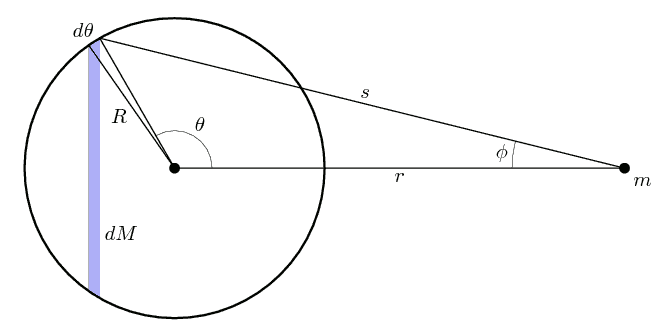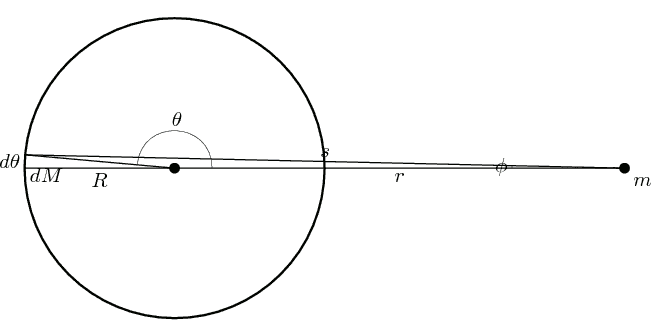
Let us for simplicity work in terms of potential energy (rather than force), because it is easier to work with a scalar (rather than a vector) quantity. We may assume that the contribution $dU$ to the potential energy of the mass $m$ and $dM$ with distance $s$ is of the form
$$ dU~=~m~dM~u(s),\tag{1.1}$$
where $s\mapsto u(s)$ is an unknown specific potential. Define for later convenience the antiderivative
$$V(s)~:=~\int^s\! ds^{\prime}~s^{\prime}~ u(s^{\prime}), \tag{1.2}$$
so that
$$V^{\prime}(s)~\stackrel{(1.2)}{=}~s~u(s).\tag{1.3}$$
From geometry we have the cosine relation
$$ \cos\theta ~=~\frac{r^2+R^2-s^2}{2rR},\tag{1.4} $$
and therefore
$$dM ~=~ \frac{M}{2}\sin\theta~ d\theta ~=~-\frac{M}{2}~d\cos(\theta) ~\stackrel{(1.4)}{=}~\frac{M}{2}\frac{s~ds}{rR}.\tag{1.5}$$
In the last equality of eq.(1.5) we varied $s$ and $\theta$ while holding $r$ and $R$ fixed. Then we have
$$dU~\stackrel{(1.1)+(1.5)}{=}~\frac{mM}{2}\frac{s~ds}{rR}~u(s) ~\stackrel{(1.3)}{=}~\frac{mM}{2rR}ds~V^{\prime}(s).\tag{1.6}$$
So the total potential energy is
$$U(r,R)~=~\int dU ~\stackrel{(1.6)}{=}~mM\frac{V(r+R)-V(r-R)}{2rR}$$ $$~\stackrel{(1.8)}{=}~\frac{mM}{r}\left(V^{\prime}(r)+ \frac{R^2}{6}V^{\prime\prime\prime}(r)+ {\cal O}(R^5)\right).\tag{1.7}$$
In the last equality of eq. (1.7), we Taylor-expanded the potential
$$V(r\pm R)~=~V(r) \pm RV^{\prime}(r) + \frac{R^2}{2}V^{\prime\prime}(r) \pm \frac{R^3}{6}V^{\prime\prime\prime}(r)+ {\cal O}(R^4). \tag{1.8}$$
Let us now implement the main converse shell assumption: We assume that the potential energy $U(r,R)$ up to an ambiguity in the choice of zero-point energy $U_0(R)$ does not depend on the radius $R$ of the thin shell, i.e. $U(r,R)$ is of the form
$$U(r,R)~=~U_1(r)+U_0(R) .\tag{1.9} $$
We see that the only way that eq. (1.7) could be of the form (1.9) is iff
$$ V^{\prime\prime\prime}(r)~\stackrel{(1.7)+(1.9)}{\propto}~r,\tag{1.10} $$
i.e. $V^{\prime}$ is a 3rd-order polynomial with a missing 2nd-order term:
$$ V^{\prime}(r)~\stackrel{(1.10)}{=}~Ar^3+Br^2+Cr+D\tag{1.11}, \qquad B~=~0. $$
Or in terms of the specific potential
$$ u(r)~\stackrel{(1.3)+(1.11)}{=}~Ar^2+C+\frac{D}{r}\tag{1.12}. $$
Or in terms of the specific force
$$ -f(r)~=~u^{\prime}(r)~\stackrel{(1.12)}{=}~2Ar-\frac{D}{r^2}\tag{1.13}. $$
$\Box$
This follows from Gauss's law. The $1/r^2$ part would be for a Gaussian sphere of radius greater the radius if the source, while the $r$ part follows from having a Gaussian sphere with radius inside the source, assuming uniform mass density.
The best way to show this is to start from the differential equation for the potential in spherical coordinates assuming spherical symmetry; this would be the Laplace equation outside and the Poisson equation with a constant term on the right inside the source. Once you have the potential you can get the force through the gradient.
Edit. Start from \begin{align} \nabla^2V(r)&=0\, ,\\ \frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{dV}{dr}\right)&=0\, ,\\ r^2\frac{dV}{dr}&=-a\, , \end{align} for some constant $a$. This is enough to give you the force as $\sim 1/r^2$ outside the source since $F_r=-\frac{dV}{dr}$.
Inside, you need to find a particular solution to $$ \nabla^2V=4\pi G\,\rho_m $$ where $\rho_m$ is the mass density. By inspection $dV/dr=4\pi G\rho_m\,r/3$ will work; this entails $F_r=br$ inside the source. The general solution with $\rho_m\ne 0$ is then the sum of the particular solution and the sum of the homogenous problem.