Placing points on a sphere so that no 3 lie close to the same plane
I do not think you expect to find an optimal configuration. I will describe a general idea to produce a reasonable one. Hope someone will give you a better answer.
In the answer I looking for a configuration of points on the plane such that angles between lines through pairs of these points are big enough. This construction can be modified easily for your needs.
Fix some natural number $N$. Choose a half-circle $\gamma$. Let $M$ be the number of integer points on $\gamma$ with all coordinates in $[0,N]$. One can choose $\gamma$ so that $M$ is quite big; say $M\gg C\cdot N^{2/5}$ is easy to arrange, but one can do better.
Note that for any two distinct pairs $(x,y)$ and $(v,w)$ of integer points on $\gamma$ we have $$|(y-x)+(w-v)|\ge 1.$$
For each integer point $x=(x_1,x_2)\in\gamma$, consider the number $$\bar x=x_1+(2\cdot N)\cdot x_2$$ All $\bar x$'s form a set $\bar X$ of integers in $[0,(2\cdot N)^2]$ such that for any two distinct pairs $(\bar x,\bar y)$ and $(\bar v,\bar w)$ of numbers in $\bar X$, we have $$|(\bar y - \bar x)+(\bar w - \bar v)| \ge 1.$$
Mark all points on a circle with central angles $\tfrac{\bar x\cdot\pi}{(2\cdot N)^2}$, $\bar x\in \bar X$. Note that the angles between the lines through these points will be $\ge \tfrac{\pi}{2\cdot (2\cdot N)^2}$.
If you look for a set of $n$ points, you it sufficient to take $N\gg n^{5/2}$ and therefore the angle will be $\gg 1/n^5$. This estimate can be improved, but I do not think you can get $\gg 1/n^2$ on this way; this might be the optimal asymptotic (?).
This is not an answer, just a remark.
I find your question interesting even for small values of $n=|V|$.
For example, if $n=4$, then choosing $V$ as the vertices of a regular tetrahedron,
the $\binom{4}{2}=6$ planes $V_P$ determine six normal lines that define a cuboctahedron:
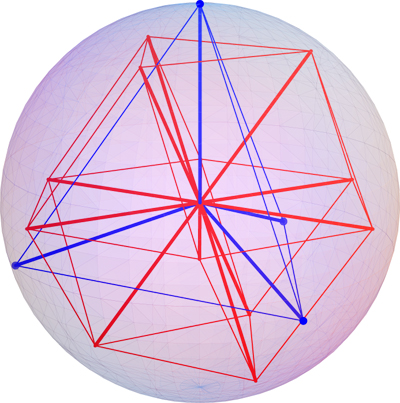
The angles between these lines/planes is either $90^\circ$ or
about $63.6^\circ$ (or $116.4^\circ$) $60^\circ$ (or $120^\circ$).
Now, the optimal packing of six lines is known (Conway, Hardin, Sloane) to be the six diameters of the icosahedron.
The minimum angle determined by those diameters is a bit larger, if I've calculated
correctly: $63.4^\circ$.
So: Is there an arrangement of four vectors $V$ that yields this optimal line packing? Answer: No, $60^\circ$ is the optimal for $n=4$. See Henry Cohn's argument in the comments.
Here is Edmund's suggestion for $n=6$: $V$ is given by half the vertices of an icosahedron (blue), which generate 15 normal lines (red) passing through the midpoints of the icosahedron's 30 edges, with the normal lines separated by $49.7^\circ$.
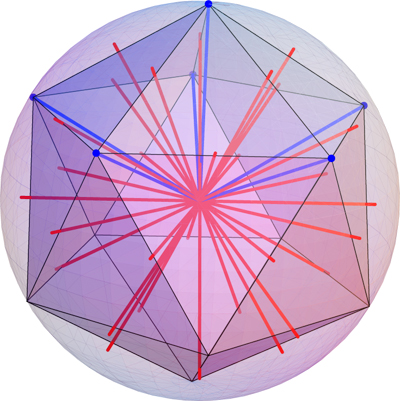
The tips of the normal lines form the vertices of an icosidodecahedron.