$\mathrm{Bessel}^3$ Integral

In fact, precisely your integral has been computed in closed form, in: Annie Gervois and Henri Navelet, Some integrals involving three Bessel functions when their arguments satisfy the triangle inequalities, J. Math. Phys. 25 (1984), no. 11, 3350–3356. Their result is $$ \int_0^\infty J_m(ar)J_n(br)J_{m+n}(cr)r\,dr = \begin{cases} 0&\text{if }c^2 < (a-b)^2\\ \dfrac{\cos(mB-nA)}{\pi ab\sin C}&\text{if }c^2 = a^2+b^2-2ab\cos C\\ 0&\text{if }c^2 > (a+b)^2 \end{cases} $$ where in the second case, $A, B, C$ are the angles opposite to sides $a, b, c$ of the resulting triangle. (They give formulas valid for real $m, n$, which reduce to the above when $m, n\in\mathbf Z$ as you assume.)

To put this in your notation, take $(m,n,a,b,c)=(l_0,-l_1,k_0,k_1,k)$ and use that $A+B+C=\pi$ and $J_n=(-1)^nJ_{-n}$. We get $$ \int_0^\infty J_{l_0}(k_0r)J_{l_1}(k_1r)J_{l_0-l_1}(kr)r\,dr = \begin{cases} 0&\text{if }k < |k_0-k_1|\\ \dfrac{\cos([l_0-l_1]K_1-l_1K)}{\pi k_0k_1\sin K}&\text{if }|k_0-k_1|<k<|k_0+k_1| \\ 0&\text{if }k > |k_0+k_1| \end{cases} $$ where $K_0,K_1,K$ are the angles opposite to $k_0,k_1,k$. The denominator is $2\pi$ times the triangle's area.

This triple-Bessel integral was studied in much detail by S.K.H. Auluck, On the Integral of the Product of Three Bessel Functions over an Infinite Domain. Closed form expressions are given if two the three orders coincide. For the more general case, a reliable way to evaluate this integral using Mathematica is described and tested. The numerical difficulties arise because the integral diverges when $k\rightarrow|k_0\pm k_1|$.

When considered as a function of $k_0,k_1,k$, the triple-Bessel integral is sharply peaked at $k\rightarrow|k_0\pm k_1|$, and can be approximated (in the sense of a distribution) by a sum of delta functions at these points:

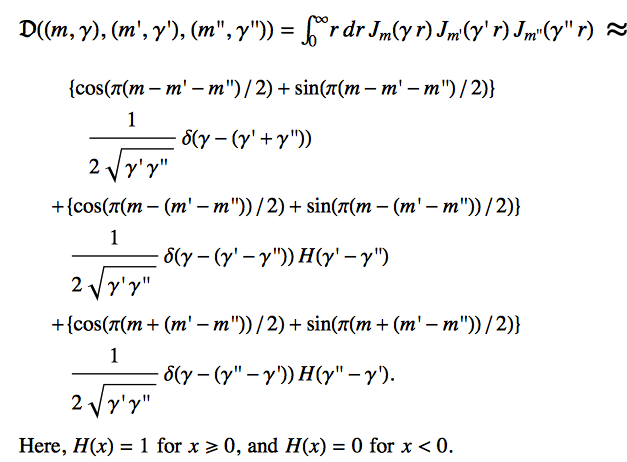
Applying that to your special case (where one order is the sum of the other two orders), I arrive at the following delta-function approximation:

$$\int_0^\infty \mathrm{BesselJ}[l_0,k_0r] \cdot \mathrm{BesselJ}[l_1,k_1r] \cdot \mathrm{BesselJ}[l_0-l_1,kr] \cdot r\,dr\approx$$

$$\frac{1}{2\sqrt{k_1 k}}\left[\delta(k_0-k_1-k)+(-1)^{l_0-l_1}\delta(k_0-k_1+k)H(k_1-k)+(-1)^{l_1}\delta(k_0-k+k_1)H(k-k_1)\right]$$