Is the following recursion formula for $\zeta(2n)$ known?
It's clearest to write the identities in terms of Bernoulli numbers $B_n$ using \begin{equation} \zeta (2 n) = \frac{(-1)^{n - 1} (2 \pi)^{2 n}}{2 (2 n)!} B_{2 n} . \end{equation} Remembering that $B_1 = \frac{1}{6}$ and that $B_n$ vanishes for all other odd $n$, the desired identity is \begin{equation} \sum_{k = 0}^{2 n} \binom{2 n}{k} 2^k (2^k - 1) B_k = 0 . \end{equation} In contrast, the identity of Song referred to by Carlo Beenakker is \begin{equation} \sum_{k = 0}^{2 n} \binom{2 n + 1}{k} 2^k B_k = 0 . \end{equation}
A useful reference is the book by N. Nielsen, Traité élémentaire des nombres de Bernoulli . It's necessary to convert notation from Nielsen's book using $B_n \rightarrow (-1)^{n - 1} B_{2 n}$, and use the formula for $T_n$ in equation (9) on page 56. The identity in equation (11) on page 132 is equivalent to \begin{equation} \sum_{k = 0}^{2 n} \binom{2 n}{k} 2^k B_k + 2 (2^{2 n - 1} - 1)B_{2 n} = 0 , \end{equation} which is a special case of a more general result attributed to previous authors. The identity in equation (12) on page 138 is equivalent to \begin{equation} \sum_{k = 0}^{2 n} \binom{2 n}{k} 2^{2 k} B_k + 2 (2^{2 n - 1} - 1)B_{2 n} = 0 . \end{equation} Taking the difference of these gives the desired identity.
The result is also given in equation VII on page 14 of the book by L. Saalschütz, Vorlesungen über die Bernoullischen Zahlen, which references three papers from 1843 by Stern, Schlömlich and Göpel.
One would expect a number of possible linear identities for the Bernoulli numbers. See, for example, M. W. Coffey, Bernoulli identities, zeta relations, determinant expressions, Mellin transforms, and representation of the Hurwitz numbers and references within.
I. Song, A recursive formula for even order harmonic series (1987):
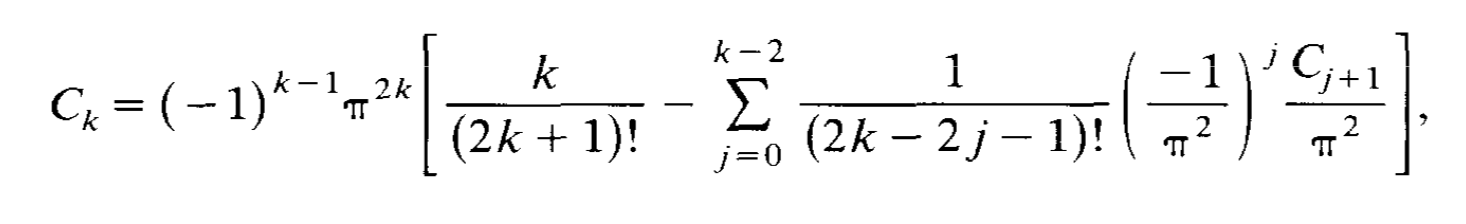
with $C_k=\zeta(2k)$. If I'm not mistaken, this is the recursion formula in the OP.