How do scientists determine when to disregard a model that has a higher correlation to data than another model?
For any set of data points, you can comprise a 100% interpolated and fitted curve using a sum of sloped lines all multiplied by their respective Heaviside step functions to form a zig-zag shaped curve. And yet, we do not use those models.
Physics from the time of Newton to now is the discipline where mathematical differential equations are used , whose solutions fit the data points and are predictive of new data. In order to do this , a subset of the possible mathematical solutions is picked by use of postulates/laws/principles , as strong as axioms as far as fitting the data.
What you describe is a random fit to a given data curve, and no possibility of predicting behavior for new boundary conditions and systems. It is not a model.
how does the academic science community of physicists know when to disregard a model that has a higher correlation than another possible model?
If one has a complete set of functions, like Fourier or Bessel functions one can always fit data curves. this is not a physics model, it is just an algorithm for recording data. The physics model has to predict what coefficients the functions that are used for a fit will have.
“Higher correlation” is meaningless beyond a certain point; namely, when both models are already so good that every data point agrees with the model prediction within the bounds of its measurement uncertainty. Then the model which gets even closer, “unnecessarily close” to the individual measurement expectation-values isn't the better model. In fact it's considered inferior, namely overfitted: some of the features in the model will be attributable to random measurement errors rather than the “inherent” system behaviour.
Now, that's not necessarily a problem. In some applications, particularly in engineering, it's perfectly fine to just measure the particular system that you're interested in and record the curve in the way you described. Then you have a very good model for that one system, and can make all the predictions as to how that system will behave in such and such state. It's a bit of an “expensive” model, in the sense that you need to store a sizable chunk of data instead of just some short formula, but hey – if you're an engineer and your customers are happy then who cares?
Things are a bit different in physics though. Here, we seek to make all laws as general as they can possibly be. Most things we can measure in the lab aren't really what we want to describe, but more of a simplified prototype to the stuff we're really interested in (but can't measure directly). So basically what we want to do is extrapolate lab results to the real world. Now, extrapolation is a dangerous business
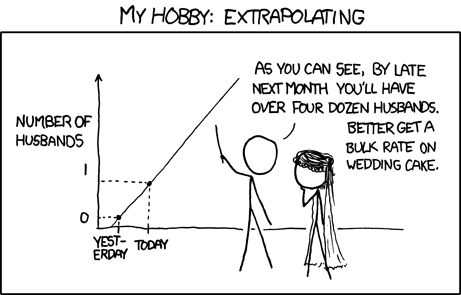
...in particular, different models that fit the same data may give rise to wildly different extrapolations. So how can we know which such model is actually going to give correct predictions?
The answer is, we can't – if we knew the correct values that are to be predicted, we wouldn't need to extrapolate in the first place! However, we can apply Occam's razor and that tends to be really quite effective at this business. Basically the idea is: a complicated model that requires lots of fitting parameters is not a good bet for extrapolation (if you can find one such model, it's likely also possible to find a similar- but differently structured model that behaves completely different as soon as you leave the original measurement domain). OTOH, a simple, elegant model given by e.g. as simple differential equation has good chances of being the only such simple model that's actually able to fit the data, hence you can be optimistic that its extrapolations will also be close to a more accurate, wider expectation window.
Two thoughts come to mind:
A theory has to describe more than one data set. If you fine tune your "theory" to fit one experiment perfectly, it most probably will fail on another one. In particular, if you consider different types of experiments (say, you measure the fall of an apple and the motion of the moon).
A theory should have some beauty. This means, there should be some simple concept behind it, so you have the feeling that it "explains" things rather than just giving an incomprehensive formula which fits to the experiment. Of course, no theory can explain everything, every theory needs some axioms, some ansatz. But the better theory explains more observations with less assumptions.