Expected determinant of random symmetric matrix with different Gaussian distributions of the diagonal and non-diagonal elements
Here is a another approach. For convenience I write $n$ instead of $N$, and $A_n$ for $A$.
By definition
$$\det(A_n) = \sum_{\pi\in S_n} \operatorname{sign}(\pi) \prod_{i=1}^n a_{i,\pi(i)}$$
By assumption $A_n$ is symmetric and the $a_{i,j}$ are (for $j\geq i$) mutually independent random variables $X_{i,j}$ with $\mathbb{E}(X_{i,i})=p=:a$, $\mathbb{E}(X_{i,j})=p^2=:c$, and $\mathbb{E}(X_{i,j}^2)=p^4 +\frac{p^2(1-p^2)}{n}=:b$ for $j\not =i$.
Denote by $C(\pi)$ the set of cycles of $\pi$ and write $\prod_{i=1}^n X_{i,\pi(i)}= \prod_{C \in C(\pi)} X_C$, with $X_C:=\prod_{i\in C} X_{i,\pi(i)}$. The cycles are disjoint, thus the different $X_C$ are independent, further $$\mathbb{E}(X_C)=\left\{ \begin{array}{cr} a &\mbox{ if $C$ is a fixed point}\\ b &\mbox{ if $C$ is a 2-cycle (transposition)}\\ c^{|C|} &\mbox{ if the length $|C|$ of $C$ is $\geq 3$}\end{array}\right.$$
To use that, denote by $Z_i(\pi), \,1\leq i\leq n$ the no. of cycles of length $i$ of $\pi$ and by $Z(\pi)=\sum_{i=1}^n Z_i(\pi)$ denote the total no. of cycles of $\pi$, and recall that $\operatorname{sign}(\pi)=(-1)^{n-Z(\pi)}$ ( "a permutation $\pi\in S_n$ is even iff it's decrement $n-Z(\pi)$ is even"). We then have
$$\mathbb{E}\det(A_n)=\sum_{\pi\in S_n} (-1)^{n-Z(\pi)} a^{Z_1(\pi)} b^{Z_2(\pi)} c^{n-Z_1(\pi)-2Z_2(\pi)}$$
It is well known how to handle this type of sums. Standard generating function techniques (see e.g. section 5.2 in Stanley's EC 2) show that $$\sum_{\pi \in S_n} t^{Z(\pi)} t_1^{Z_1(\pi)}\ldots{t_n}^{Z_n(\pi)}=n! [z^n] e^{\sum_{i=1}^n t\,t_i\frac{z^i}{i}}$$ Using that and simple manipulations we find $$\mathbb{E}\det(A_n)=n!\,[z^n] (1+cz)\,e^{(a-c)z-(b-c^2)\frac{z^2}{2}}$$ The Hermite polynomials $He_n(x)$ are defined by $He_n(x)=n![t^n] e^{xt-\frac{t^2}{2}}$. Now note that with $v:=b-c^2$ (the variance of the off-diagonal matrix elements) and $d:=a-c$ (the difference of the expectations) you have $$\mathbb{E}\det(A_n)=\sqrt{v^n}\,He_n(\frac{d}{\sqrt{v}})+cn\sqrt{v^{n-1}}\,He_{n-1}(\frac{d}{\sqrt{v}})$$
The asymptotic properties of the Hermite polynomials have been intensively investigated, so you can probably find precise results for your concrete setting in the literature.
EDIT: Note that this doesn't answer your question for the expectation of the absolute value of the determinant (thanks to Carlo Beenakker for pointing this out). I'll still leave it here in case someone's interested in the expectation of the determinant.
If I may ignore the fluctuations for large $N$, I can use that the average matrix $\bar{A}=E(A)$ has $N-1$ eigenvalues equal to $p(1-p)$ and one eigenvalue equal to $p(1-p)+Np^2$. The determinant then equals $${\rm det}\,\bar{A}=Np^{N+1}(1-p)^{N-1}+ p^N(1-p)^N.$$ Notice that it is positive definite. It decays exponentially $\propto e^{-\alpha N}$ with exponent $\alpha=-\ln p-\ln(1-p)$.
To assess the effect of the fluctuations I might consider the matrix $\delta A=A-\bar{A}$, where the matrix elements have zero average. The eigenvalues $\lambda_n$ of $\delta A$ are distributed according to the Wigner semicircle in the interval $|\lambda|<2p(1-p)$. That determinant can be at most $2^{-N}$ in absolute value, which also decays exponentially.
Update, following esg 's answer:
For $p\lesssim 1/2$ the Hermite polynomial formula (blue, absolute value of esg 's answer$^*$) is not far from ${\rm det}\,\bar{A}$ (gold, above formula), see the plot for $p=0.4$ (at left) and for $p=0.05$ (at right):
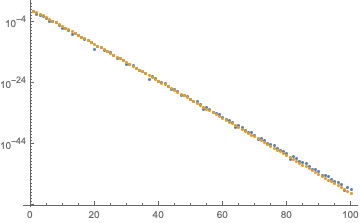
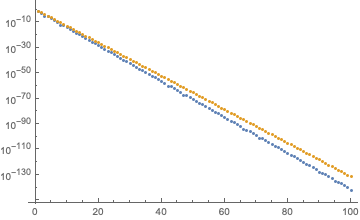
For $p>1/2$ the Hermite polynomial formula decays less rapidly, but still exponentially: plots for $p=0.7$ (at left) and for $p=0.95$ (at right). The difference from the exponent $\alpha$ given above is close to a factor 1/2 for $p$ approaching 1 (compare with green curve $\propto (1-p)^{N/2}$).
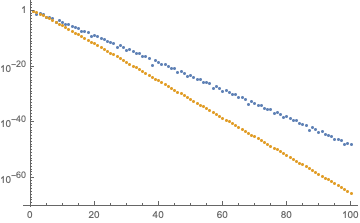
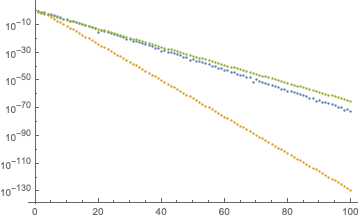
In summary, based on this comparison I would conclude that the exponential decay of $\mathbb{E}\,({\rm det}\,A)$ crosses over from $\propto p^N$ for $p$ near 0 to $\propto(1-p)^{N/2}$ for $p$ near 1.
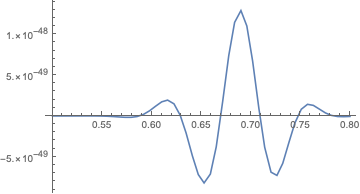
$^*$ I plotted the absolute value of the Hermite formula. It oscillates around zero with increasing $p$, here is for example a plot for $N=100$.
There is a similar question here : Expected value of determinant of simple infinite random matrix
I rewrite the heuristique from the random matrix theory: $$A=p^2 1 + (p-p^2)I_N+\sqrt{p^2(1-p^2)}\tilde{A}+\frac{1}{\sqrt{N}}D$$
where $1$ is the matrix with entries all equal to 1, $D$ a diagonal matrix with bounded variance. And $A$ is a matrix iid random entries with zero mean and variance $1/N$. Therefore its eigenvalues should be distributed similarly as the semicircul law. Because the first matrix is a rank one perturbation and $\| \frac{1}{\sqrt{N}}D \|$ is small, we could ignore them at first approximation. $$\frac{1}{N}\log(|\det(A)|)\sim \frac{1}{N}(\log(|\det(\frac{p-p^2}{\sqrt{p^2(1-p^2)}}I_N+\tilde{A}))|)+\log(\sqrt{p^2(1-p^2)}) $$ We now use the semicircul law and we should get $$\frac{1}{N}(\log(|\det(\Lambda I_N+\tilde{A})|))=\frac{1}{N}\sum_{\lambda \in \sigma (\tilde{A})} \log (|\Lambda+\lambda|) \sim \int_{-2}^{2} \log(|\Lambda+\lambda|) \rho(\lambda) d\lambda$$ where $\Lambda=\frac{p-p^2}{\sqrt{p^2(1-p^2)}}$ and $\rho(\lambda ) = \frac{\sqrt{4-\lambda^2}}{2\pi}$ is the semicircul law. So finally we should obtain $$\frac{1}{N}\log(|\det(A)|)\sim \log(\sqrt{p^2(1-p^2)})+\int_{-2}^{2} \log(|\Lambda+\lambda|) \rho(\lambda) d\lambda$$